48. 旋转图像

一、题目原型：

给定一个 n × n 的二维矩阵表示一个图像。将图像顺时针旋转 90 度。

说明：
你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

二、示例剖析：

示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵，使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
示例 2:
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵，使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]

三、解题思路：

原题题意，我们把n*n的数组想象成一个正方形，我们顺时针旋转正方形的时候，最后得到的就是旋转后的新数组。
乍一看很简单，因为有很多规律可以找到。
比方说示例1，第一行123，变成了新数组的最后一列；第二行456，变成了新数组的倒数第二列；第三行789，变成了新数组的第一列。
我们完全可以用一个临时数组将每一行抽取出来，再根据该规律，加入到新数组中。

![推算笔记](http://dancheclassmate.cn/2018/09/21/leetCode题库笔记/48--旋转图像/推算笔记.png)

然后发现，全乱了。。。问题原因应该是在相互赋值时，i和j的遍历会重复，反正方法是不对的。

接下来我想，既然一步完成不了，就分几步来做吧。
1.```上下置换```，将最上面的一排放到最下面，第二排放到倒数第二排。

[
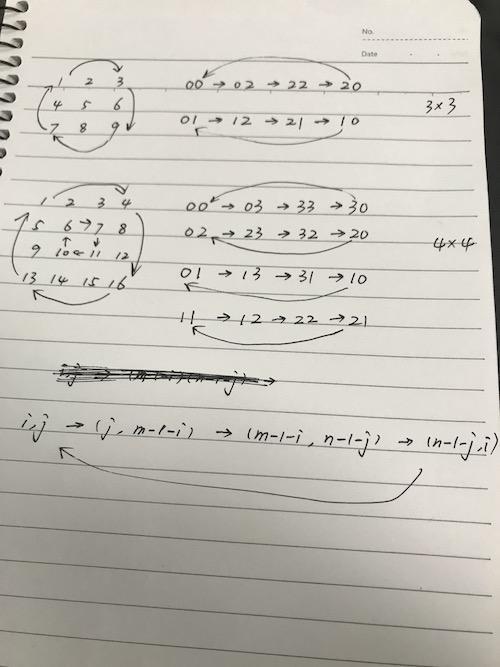[1,2,3],
[4,5,6],
[7,8,9]
],

变成

[
[7,8,9],
[4,5,6],
[1,2,3]
],

1
2

var i: Int = 0
var j: Int = 0
let m = matrix.count
let n = matrix[0].count
while j < n {

while i < m/2 {
    let temp = matrix[i][j]
    matrix[i][j] = matrix[m-1-i][j]
    matrix[m-1-i][j] = temp
    i = i + 1
}
j = j + 1
i = 0

}
print(“i = (i) j = (j) (matrix)”)

1	2.根据中间的753这条斜线对称。

[
[7,8,9],
[4,5,6],
[1,2,3]
],

变成

[
[7,4,1],
[8,5,2],
[9,6,3]
],

```
i = 0
j = 0
while j < n - 1 {
    while i < m {
        if (i >= j) {
            let temp = matrix[i][j]
            matrix[i][j] = matrix[j][i]
            matrix[j][i] = temp
            print("i = \(i) j = \(j)            \(matrix)")
        }
        i = i + 1
    }
    j = j + 1
    i = 0
}

四、小结

耗时72毫秒，超过73.77%的提交记录，总提交数504。